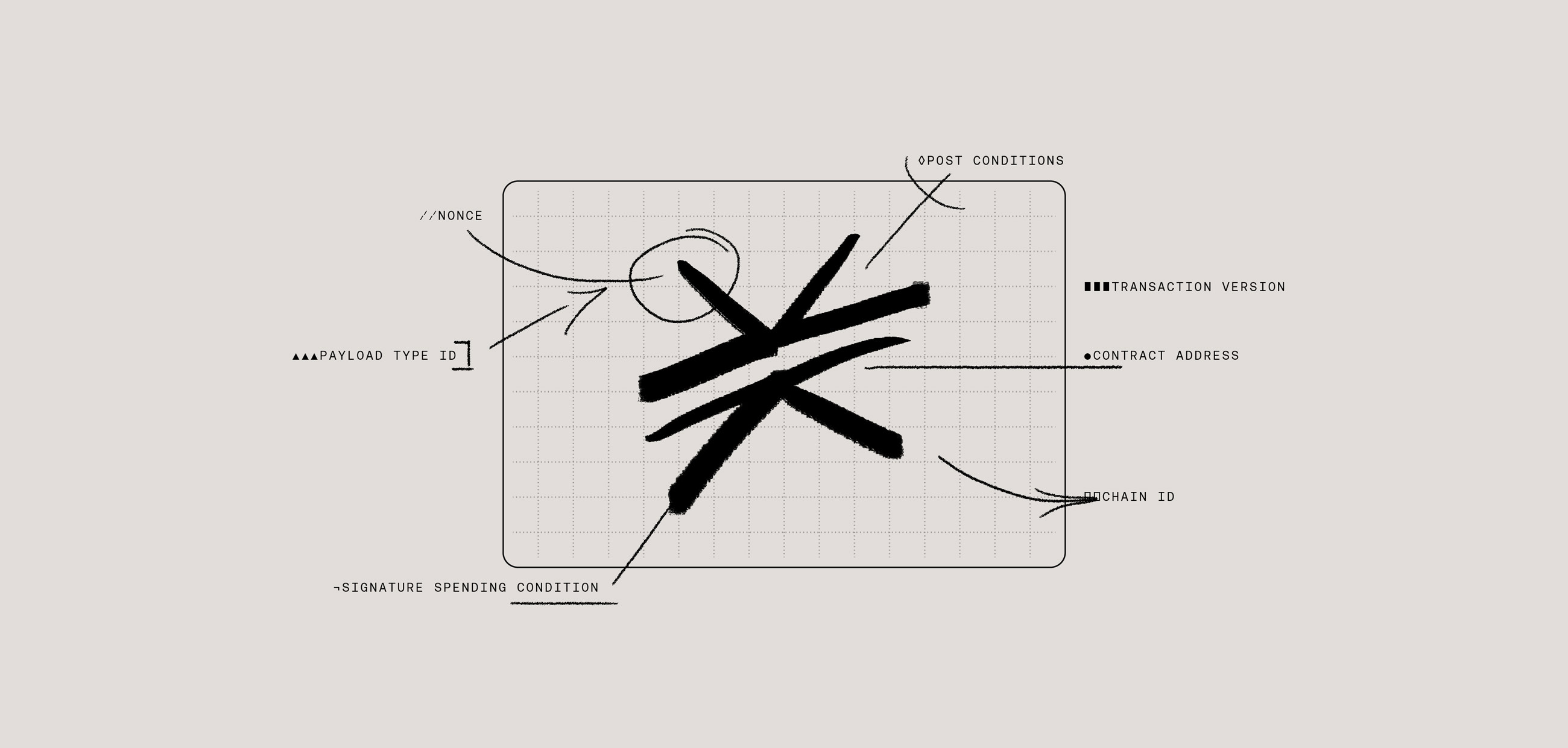
The latest Stacks network upgrade, version 2.05, resulted in fuller blocks and higher throughput. A critical component of this upgrade involved updating the constants used by Clarity cost functions. These cost functions are used by STX miners to calculate the cost of every transaction, and ultimately determine how densely they can fill their blocks.
The improved constants resulted in a 300% increase in the average block capacity. The undertaking of calculating these new cost constants was dubbed internally at Hiro as the “cost function benchmarking” project, and in this post, we will cover what we accomplished.
Background on Transaction Costs
Clarity is the programming language for writing smart contracts on the Stacks blockchain. Each block in the chain executes transactions. While some transactions simply transfer value from one account to another, more complicated transactions can run and publish code (smart contracts).
Executing these smart contract transactions is not free, however. The combined computational cost of a block’s transactions must not exceed the block’s cost limit. This cost limit is enforced to ensure that blocks are mined and processed in a consistent and timely fashion. That way blocks can be processed by nodes running commodity hardware, which ensures that the Stacks chain remains accessible to the public, and the Stacks chain can keep pace with the Bitcoin chain (if Stacks blocks were allowed to take an arbitrarily long time to process, the chain wouldn't keep up with the underlying Bitcoin chain).
To maximize network throughput, STX miners use cost functions to determine the computational cost of every transaction and calculate how densely they can fill each block.
How Do Cost Functions Work?
Obtaining the cost of a transaction that executes Clarity code is done by invoking the cost functions that correspond to each Clarity function that is called. These cost functions compute the approximate cost of executing a Clarity smart contract. Clarity cost functions are simple arithmetic expressions. They are typically either constant values, linear functions, or functions of the form alog(n) + b or a(nlog(n)) + b.
The output of these functions is an object that contains five cost values: runtime, write length, write count, read count, and read length. In practice, most of these costs are constant values, except for runtime. This cost function benchmarking project was concerned with determining these runtime cost functions for different transaction types.
The runtime cost functions represents the relationship between the size of the input and the amount of compute required to execute the function (aka the runtime cost). These functions can be thought of much like the Big O notation that is often used to describe how an algorithm's runtime (or space) requirements grow as the input size grows.
For the 2.0 release of the blockchain, these cost functions were all deliberately set with excessively large constants. This prevented the network from being overloaded early on in its existence, a precaution we took to account for unforeseen engineering challenges. Through the Clarity benchmarking project, we have obtained more accurate, and generally smaller, values for these constants, which lowers computed runtime costs, resulting in fuller blocks and significantly higher network throughput.
The Project
High Level Approach
In order to determine accurate runtime cost functions for Clarity, we needed to isolate and benchmark each of Clarity's native functions. To do this, we used Criterion, a statistics-driven benchmarking library for Rust. Criterion is a powerful tool for detecting and measuring the performance of Rust code. We were able to use Criterion to benchmark Clarity code because the Clarity virtual machine is implemented in Rust.
For almost every native Clarity function, we wrote a code generator. Each code generator created a Clarity code snippet invoking the function being benchmarked with a specified input size. Once we generated a Clarity code snippet, we interpreted the code string into an AST (abstract syntax tree), setup an environment for executing the code, and finally executed and benchmarked the code with Criterion.
Criterion runs a suite of these benchmarks sequentially and automatically runs many iterations of each, taking the average result for a more accurate output. The output of these benchmarks gets stored in a CSV file that is ultimately analyzed to compute each Clarity cost function's specific constants. We did this analysis with a Python script that utilizes the scientific computing libraries numpy, pandas and scikitlearn.
Benchmarking the Cost Function and
For a simple example, we can consider the cost function cost_and, which corresponds to a clarity function and. The and function is variadic, meaning it can take any number of inputs, and returns true only if all of its inputs evaluate to true. Here is an example of it being invoked:
The cost function cost_and is linear, taking the form mx + b. This means that the total cost of invoking and grows linearly with the number of arguments supplied. To obtain the constants m and b, we need to benchmark the and function with various input sizes. Then, we fit a line to the measured outputs using a linear regression. The slope of this line is our m value and the y-intercept is b.
For the cost function And, we collected runtime data for the following input sizes: 1, 2, 8, 16, 32, 64, 128, 256. We dynamically generated clarity code snippets corresponding to each input size. For example, a code snippet corresponding to input size 4 might look like:
In order to offset the costs associated with the startup time of the clarity virtual machine itself, we generate these code snippets where the benchmarked function is repeatedly invoked (as you can see in the above snippet). The number of repetitions is controlled by a configurable SCALE parameter. After running the benchmark, we normalized the data to obtain the cost function constants.
It Gets Complicated…
At first glance, this process seems pretty simple. We just need to write code generators for every Clarity function and benchmark the code, right? Well, yes... But not every function is as simple to benchmark as and. Certain Clarity functions expect some sort of local contract state or global chain state to exist. For example, in order to benchmark the map-get? function, we need a map to have been defined, or in order to benchmark block-info, we need to have some sort of chain state where multiple blocks have been mined.
For Clarity functions that simply reference local contract state, it is sufficient to run a snippet of setup Clarity code before the benchmark gets run. For some functions like block-info we need to simulate a Clarity "HeadersDB" (the database that stores information about stacks and burn block headers).
Moreover, there isn’t a one to one correspondence between Clarity functions and cost functions. Some cost functions are used to compute the costs of analyzing Clarity code. For example, there are cost functions associated with type checking Clarity code. Here is a list of the cost functions that are invoked when the clarity function map-set is analyzed.
- CostAnalysisVisit: cost of calling the function type_check.
- CostAnalysisTypeAnnotate: cost of setting the type signature of both the key & value type in the type checker’s type map (proportional to the size of the type signature).
- CostAnalysisTypeLookup: cost of looking up the expected type of the key and value of the map (proportional to the type size of each).
- CostAnalysisTypeCheck: cost of checking that the key and value are admitted by the expected type for each (proportional to the size of the expected types).
To create benchmarks for cost functions that didn't cleanly correspond to a single Clarity function, we forked the Stacks blockchain codebase and wrote benchmark specific functions that isolated the logic we were trying to measure. We then ran benchmarks on these contrived functions to obtain the constants for these more specific cost functions.
Crunching the Numbers
The output from running the benchmarking suite captures the measured runtimes for the benchmarks for every cost function, often on a range of input sizes.
Here is a selected snippet of the raw numerical results (not all possible input sizes nor cost functions are shown below), which are in nanoseconds:

Before plotting these numbers, we had to transform the raw data. First, we divided all the numbers by the SCALE parameter (which was in this case 75) to compensate for the repeat computation performed (described in the earlier section). Second, we needed to normalize the units to correspond to the node's notion of "runtime", since that is what we must measure costs in. Ultimately, "runtime" is measured in an arbitrary unit. Each block has a set total runtime limit, which needs to correspond to roughly 30 seconds of execution time. We scaled the data such that this requirement held true.
For the cost functions that take an input size argument, we plotted the results and obtained a line of best fit via linear regression. We ultimately derived the cost function constants from these lines (you can see the code we used to do this here). In order to perform a linear regression on data for cost functions which are not linear (in our case either nlog(n) or log(n)) we must transform the X axis of the data with the applicable nonlinear function first.
Here is an example of one of these plots, for the cost function cost_analysis_iterable_func:

For the same cost functions we gave the runtimes for above, here are the computed constants. These are the same values that were ultimately proposed in SIP-012. “a” and “b” represent the values we substitute in to a generic arithmetic function. For example, if a particular cost function corresponds to the expression cost = alog(n) + b, we would substitute the computed constants a and b into the function to obtain the function relating input size, n, to the cost.

To put these improvements into context, here is the same table but with the old constants, pre-benchmarking:

Wrapping Up
The Clarity benchmarking project yielded more accurate and mostly smaller constants for all of the Clarity cost functions. The results have been put to use in the newest release of the Stacks blockchain, which aims to increase the throughput of the network. In this case, more accurate cost functions means more transactions in each block, which alleviate one of the current major pain points for developers, miners, and users alike, which is the need for higher network capacity.
The newest release of the blockchain does not mark the end of this benchmarking project: we will extend the repo in order to calculate cost constants for Clarity functions added to the language in the future. If interested in future developments, you can follow the project here.
After months of work obtaining these new cost functions, we can't wait to see the innovation the 2.05 network upgrade will enable on the Stacks blockchain!